AUTHOR: Md. Motiur Rahman
SUPERVISOR: Dr. Debasish Sarker
PROGRAM: Bachelor of Science in Mechanical Engineering
DEPARTMENT: Department of Mechanical Engineering
INSTITUTION: International University of Business Agriculture and Technology
SUBMISSION: Summer, 2023
ABSTRACT: Ceiling fans are commonly used in tropical climates to provide comfort in domestic buildings. Although fan energy consumption is relatively low in comparison to air conditioning, it suffers from some degree of electricity loss which is mainly due to its mechanical inefficiency. This paper illustrates a theoretical and mathematical approach for designing an efficient ceiling fan blade. This new design has been evaluated by computational fluid dynamics (CFD).
KEY WORDS: Momentum theory, Blade element theory, Lifting line theory, Computational fluid dynamics (CFD), Ceiling fan blade design
Blade Design Parameters
| Airfoil | NACA 2410 |
| Angel of Attack, \(\alpha\) | 4.5° |
| Chord, \(C\) | 0.1 m |
| Blade Number, \(N\) | 3 |
| Hub Diameter, \(r_{hub}\) | 0.13 m |
| Blade Span, \(b\) | 0.56 m |
| Blade Tip, \(R\) | 0.7 m |
3D CAD Model of Ceiling Fan with Optimized Blade.
Problem Statement
During my undergraduate thesis, my supervisor challenged me to design a ceiling fan blade—an apparently simple device that quietly shapes everyday comfort. Motivated by curiosity and enthusiasm, I began searching for established theories and design equations to guide the process. Surprisingly, despite the ubiquity of ceiling fans, I found no dedicated or well-developed theoretical framework tailored to their aerodynamic design. This gap became the driving force of my work. As a result, I set out to develop an original mathematical formulation for an energy-efficient ceiling fan blade, drawing upon advanced aerodynamic concepts such as momentum theory, blade element theory, and lifting-line theory.
Assumptions
- The flow is steady-state and incompressible.
- The rotor experiences a uniform inflow velocity.
- The blade has a constant chord length along its entire span.
- The blade operates at a fixed angle of attack relative to the resultant flow.
- The lift and drag coefficients are assumed to be constant along the blade span.
Nomenclature
Inflow Velocity at Rotor, \(V [m/s]\)
Rotor Thrust, \(T [N]\)
Rotor Torque, \(Q [Nm]\)
Angular velocity of Rotor, \(\Omega [rad/s] \)
Radius of Rotor, \(R [m]\)
Rotor Hub Radius, \(r_{hub} [m]\)
Number of Blade, \(N\)
Chord Length of Blade, \(C [m]\)
Span of Rotor Blade, \(b [m]\)
Aspect Ratio of Blade, \(AR=\frac{b}{C}\)
Optimal Angel of Attack, \(\alpha [rad]\)
Zero Lift Angle, \(\alpha_{L=0} [rad]\)
Inflow Coefficient, \(\lambda=\frac{V}{\Omega R}\)
Hub to Tip Ratio, \(\phi=\frac{r_{hub}}{R}\)
Solodity Ratio, \(\sigma=\frac{NC}{\pi R}\)
Lift Coefficient of Airfoil, \(C_l\)
Drag Coefficient of Airfoil, \(C_d\)
Lift Coefficient of Blade, \(C_L\)
Drag Coefficient of Blade, \(C_D\)
Thrust Coefficient, \(C_T=\frac{T}{\rho N C \Omega^2 R^3}\)
Torque Coefficient, \(C_Q=\frac{Q}{\rho N C \Omega^2 R^4}\)
Volume Flow Rate, \(\dot{\rlap{-}V\llap{-}} [m^3/s]\)
Aerodynamic Efficiency, \(\eta\)
Mathematical Formulation
Coefficient of lift and drag for a finite wing or blade are defined by the following equations derived from the lifting line theory.
$$C_L=a(\alpha-\alpha_{L=0}) \tag{1}$$
$$C_D=C_d+\frac{C_L}{\pi e AR} \tag{2}$$
Here, \(a\),\(a_0\), and \(e\) are defined as \(a=\frac{a_0}{1+\frac{a_0}{\pi AR}(1+\tau)}\), \(a_0=\frac{dC_l}{d\alpha}\), and \(e=\frac{1}{1+\delta}\). Where, \(\tau=\delta\) is function of Fourier transform and can be found in Funda-mentals of Aerodynamics by John D. Anderson.
The blade element theory and the momentum theory is combined into the following quadratic equation where \(\lambda\) is the variable.
$$24(1-\phi^{2})\lambda^{2}+3\sigma C_{D}\lambda-2\sigma C_{L}=0 \tag{3}$$
We can evaluate the value of \(\lambda\) by solving eqn (3) using quadratic formula.
The following equations (4) and (5) are derived from blade element theory is used to evaluate the coefficient of thrust and torque of the rotor.
$$C_T=\frac{4C_L-6C_D \lambda}{24} \tag{4}$$
$$C_Q=\frac{3C_D+4C_L \lambda}{24} \tag{5}$$
From equation (3), (4), and (5) we can evaluate the following properties of the rotor.
$$V=\lambda \Omega R$$
$$T=C_T \rho N C \Omega^2 R^3$$
$$Q=C_Q \rho N C \Omega^2 R^4$$
$$\dot{\rlap{-}V\llap{-}}=\pi R^2 V$$
The volume flow rate per unit power and aerodynamic efficiency are defined as,
$$\frac{\dot{\rlap{-}V\llap{-}}}{\Omega Q}$$
$$\eta=\frac{C_T \lambda}{C_Q}$$
CAD Model

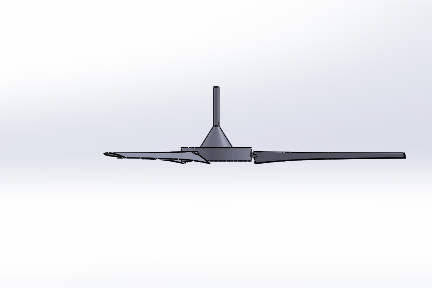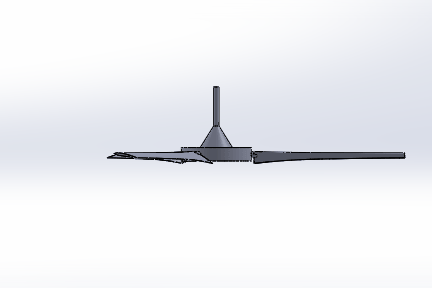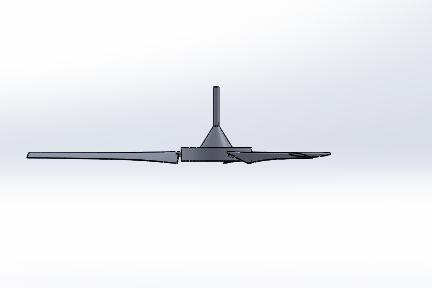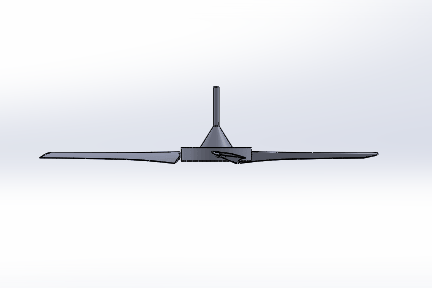
Sample 3D Ceiling Fan Model
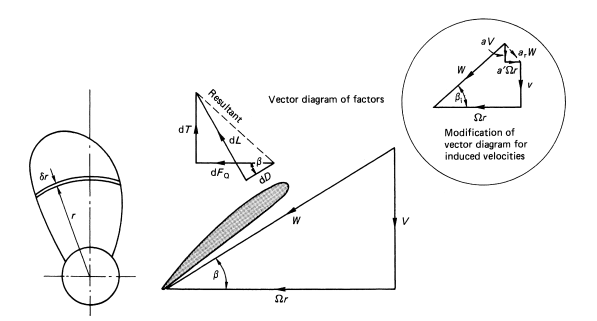
Designing the Blade
To design the blade, the pitch angle \(\left( \theta \right)\) must be calculated at various blade sections located at a radial distance \(r\) from the rotor center.
$$\theta=\beta+\alpha$$
Where, \(\beta\) is the angel of incoming air and \(\alpha\) is the angel of attack.
$$\tan{\beta}=\frac{V}{\Omega r}$$
$$\beta=\tan^{-1}{\frac{V}{\Omega r}}$$
$$\theta=\tan^{-1}{\frac{V}{\Omega r}}+\alpha$$
Conclusion
This paper focused on developing a new theoretical model for designing efficient ceiling fan blades. These mathematical equations are derived from the basic theories of aerodynamics e.g. Momentum Theory, Blade Element Theory, Lifting Line Theory, and the conservation laws of fluid dynamics e.g. Conservation of Mass, Momentum, and Energy. Some assumptions are made to simplify the problem. The validity of these equations was checked by using Numerical Methods such as CFD, the results from the numerical solutions give promising results. These equations can predict more than 90% accurate results when compared with numerical solutions. Blades designed using these equations deliver 14% more axial velocity at 1.5 m below the fan and consume 22% less energy to run.