AUTHOR: Md. Motiur Rahman
AFFILIATION: Department of Mechanical Engineering, International University of Business Agriculture and Technology, Dhaka, Bangladesh
DOI: https://doi.org/10.31224/6263
KEY WORDS: Partial magnetic field,Natural convection, Porous medium, Non-uniformly wavy cavity
ABSTRACT: This study investigates natural convection within a square porous cavity subjected to a partially applied horizontal magnetic field along a section of the left vertical wall. The top and bottom horizontal walls are thermally insulated. The left wall is maintained at a high temperature, while the opposing right wall, characterized by a varying-amplitude wavy surface, is kept at a lower temperature. The Brinkman Forchheimer-extended Darcy model is employed to simulate the fluid flow within the porous medium. The governing equations are numerically solved using the Galerkin finite element method, and the accuracy of the approach is validated through comparison with previous study. The effects of key parameters including the magnetic field length, Hartmann number, Rayleigh number, Darcy number, and the wall wave damping effect are analyzed in terms of streamlines, isotherms, and average Nusselt number. The results demonstrate that the magnetic field suppresses convective flow and reduces heat transfer, highlighting its potential for controlling thermal transport and fluid motion within porous enclosures. Furthermore, increasing the damping effect of wall waves reduces heat transfer by simplifying convective patterns.
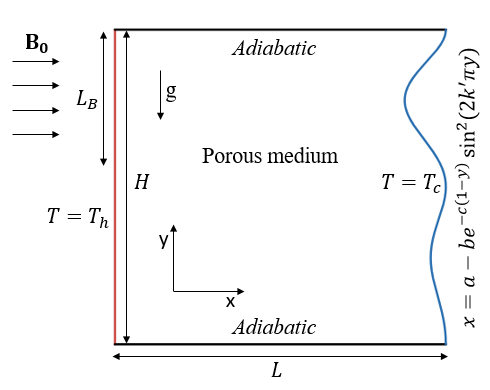
Problem Description
Method of Solution
Conclusion
This study numerically analyzed natural convection within a square wavy porous cavity under the influence of a partially applied magnetic field. Key parameters—including magnetic field length \(L_B\), Rayleigh number \(R_a\), Hartman number \(H_a\), Darcy number \(D_a\), and wave damping effect \(c\) were varied within the ranges \(L_B=0.3-0.7\),\(R_a=10^4-10^6\), \(D_a=0.0001-0.01\),and \(c=1-3\). The simulations evaluated the effects of these parameters on temperature distribution, average Nusselt number, streamlines, and isotherms. The main findings are summarized below:
- Magnetic field length: Increasing the length of the applied magnetic field reduces heat transfer. Specifically, as increases from 0.3 to 0.7, the average Nusselt number drops by .
- Rayleigh number: Higher values enhance heat transfer and fluid motion due to stronger buoyancy forces. An increase in from to results in more than a fivefold increase in the Nusselt number.
- Secondary vortex formation: At lower Rayleigh numbers, a secondary vortex appears, caused by the Lorentz force dominating over buoyancy.
- Lorentz force impact: The suppressive effect of the Lorentz force on heat transfer and fluid flow becomes more pronounced at higher Rayleigh numbers.
- Hartmann number: As increases, the Lorentz force intensifies, leading to a reduction in both heat transfer and flow strength. A rise in from 0 to 200 decreases the Nusselt number by 44%.
- Darcy number: Enhanced permeability in the porous medium significantly improves heat transfer. As increases from 0.0001 to 0.01, the Nusselt number more than doubles.
- Effectiveness of magnetic field: At low Darcy numbers, the magnetic field has minimal impact due to weak fluid motion.
- Wave damping effect: The increasing damping effect in the wave function results in reduced Nusselt number. Which validates that more curvature means more area for heat transfer therefore resulting Nusselt number is higher.